Spike Solution - Morphing Graphs
Bar charts, stream graphs and heatmaps are ubiquitous. Let's unify them.
This spike solution is a bit further on than pure raw output from Claude. The idea is that we can unify different graphs by morphing between them.
Spike 1 - Heat Map Sankey
Spike 2 - Git Flow
Spike 3 - WarpedPolygon
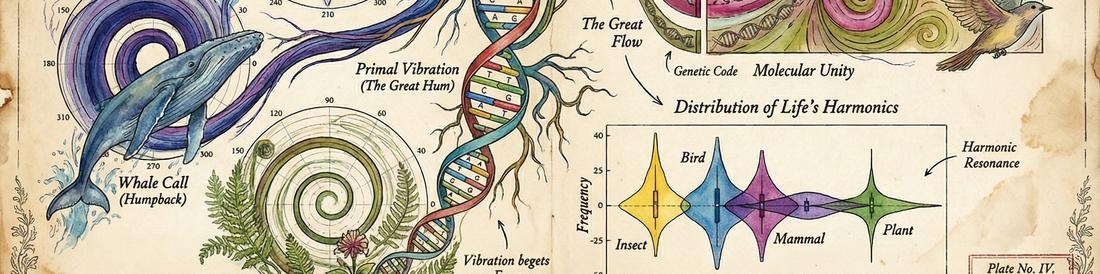
For OmniChart I needed to explain to Claude how to make a rectangle with curved edges the way I wanted - with a bend parameter, 0 for straight, for each side. The quick way to do this was to one-shot a demo of the concept, and get actual code. Then I could hand the code to another instance of Claude and say 'here's the idea'.
Log
- 17-Jan-2026: Implemented the basic OmniGraph graph set, stacked, radial, donut platter.
- 18-Jan-2026: Added WarpedPolygon spike to progress the OmniGraph
Take Homes
The first two spike solutions are cornerstones of a more complete system of morphing graphs.
- I need to adapt my existing renderer for ribbons, if I am to use it on these graphs. Claude used bezier ribbons with horizontal ends - and different code for the ribbons in the HeatMap and GitFlow versions. I need to adapt my ribbons to cover both cases.
- Some general system is needed for sparse data. The stream graph is a sparse data version of a Sankey diagram, where all the flows are 'on the diagonal'. We seem to need something that can handle both regular patterns - such as all on the diagonal - and small variations such as additional off-diagonal flows.
Built with Claude
I had a chat with Claude about how to be systematic about the different kinds of morphing between diagrams I want to do. Claude had a great tendency to expand in detail, and rather uninformatively, on what the different morphings should be doing. In the end Claude was more useful as a 'rubber ducking' than an actual helpful conceptual partner in this. It helped me realise how tooltips fit in.
Whether tooltips are shown on hover, scroll into view as needed, or are indicated by a signposting ribbon that can navigate to them, they are 'the same thing'.
I had been treating tooltips on the graphs as special and different from the nodes. I'd seen the system for info cards (the tooltips) as a completely different system to the system that makes the graphs they annotate.
The 'rubber ducking' also simplified the morphing problem. Every diagram I plan to make has nodes and ribbons connecting the nodes. Regularity often disguises the presence of ribbons, or disguises the existence of distinct nodes.
For a nodes and ribbons diagram (covers many cases) the main constraint of interest is how the ribbons are determined, when their existence is implied rather than explicitly spelled out.
For a stream graph there are implied ribbons between the categories.
I also needed standard charts before the all-singing all-dancing heatmap / sankey / barchart code would be ready. The WarpedPolygon spike solution came out of that. Claude did one shot it, but I needed to do it as a separate task, so that Claude could focus just on that task.